[New 2025-26] Chapter 2 - Lines and Angles NCERT Solutions | Worksheet | Extra Questions for Class 6 Maths Ganita Prakash.
Class 6 maths chapter 2 full chapter : Lines and Angles.
'Lines and Angles' is an important topic to understand in mathematics. In this chapter, we will explore some of the most basic ideas of geometry including points, lines, rays, line segments and angles. These ideas form the building blocks of ‘plane geometry’, and will help us in understanding more advanced topics in geometry such as the construction and analysis of different shapes...

-
# THIS PAGE INCLUDES :
# Notes : Lines and Angles
lines and angles class 6 notes
● Point :
A point determines a precise location, but it has no length, breadth or height. In geometry, we label points with capital letters like A, B, C, etc. These are read as 'Point A', 'Point B', 'Points C', etc.

● Line Segment :
A line segment (AB) has fixed length. It has 2 end points, which can be marked as A and B. The points A and B are called end points of line segment AB.

● Line :
A line (AB) has no fixed length. It has no end points, so It can be extended endlessly in both the directions beyond A and B.

● Ray :
A ray is a portion of a line that starts at one point (called the starting point or initial point of the ray) and goes on endlessly in a direction.

● Angle :
An angle is formed by two rays having a common starting point. Here is an angle formed by rays BA and BC where B is the common starting point. The point B is called the vertex of the angle, and the rays BA and BC are called the arms of the angle.

Types of Angles :
● Acute Angle :
Angles which measure less than 90° are called acute angles. The measurement of these angles are between 1° to 89°.

● Right Angle :
The angle which measure exactly 90° is called right angle. The shape of this angle is capital 'L'.

● Obtuse Angle :
Angles which measure more than 90° but less than 180° are called obtuse angles. The measurement of these angles are between 91° to 179°.

● Straight Angle :
The angle which measure exactly 180° is called straight angle. The shape of this angle is like a flat line.

● Reflex Angle :
The angles which measure more than 180° but less than 360° are called reflex angles. The measurement of these angles are between 181° to 359°.

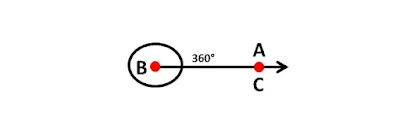
● Complete angle :
The angle which measure exactly 360° is called a complete angle. The shape of this angle is like a circle.
----- The End -----
# Key Points :
● A point determines a location. It is denoted by a capital letter.
● A line segment corresponds to the shortest distance between two points. The line segment joining points S and T is denoted by ST.
● A line is obtained when a line segment like ST is extended on both sides indefinitely; it is denoted by ST or sometimes by a single small letter like m.
● A ray is a portion of a line starting at a point D and going in one direction indefinitely. It is denoted by DP where P is another point on the ray.
● An angle can be visualized as two rays starting from a common starting point. Two rays OP and OM form the angle ∠POM (also called ∠MOP); here, O is called the vertex of the angle, and the rays OP and OM are called the arms of the angle.
● The size of an angle is the amount of rotation or turn needed about the vertex to rotate one ray of the angle onto the other ray of the angle.
● The sizes of angles can be measured in degrees. One full rotation or turn is considered as 360 degrees and denoted as 360°.
● Degree measures of angles can be measured using a protractor.
● Angles can be straight (180°), right (90°), acute (more than 0° and less than 90°), obtuse (more than 90° and less than 180°), and reflex (more than 180° and less than 360°).
# NCERT Solutions :
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 15.
Lines and Angles Class 6 NCERT Solutions Ganita Prakash Maths Chapter 2
Q1.

Can you help Rihan and Sheetal find their answers?
Solution :
● Rihan can draw infinite number of lines that pass through the point.

● Sheetal can draw only one line that pass through both the points.

Page 16 : Figure it out
Q2.
Name the line segments in Fig. 2.4. Which of the five marked points are on exactly one of the line segments? Which are on two of the line segments?

Solution :
● Points that are exactly on one line segment : 'L and R'
L : Point 'L' is exactly on line segment LM.
R : Point 'R' is exactly on line segment QR.
● Points that are on two line segment : 'M, P and Q'
M : Point 'M' is on two line segments LM and MP.
P : Point 'P' is on two line segments MP and PQ.
Q : Point 'Q' is on two line segments PQ and QR.
Q3.
Name the rays shown in Fig. 2.5. Is T the starting point of each of these rays?

Solution :
In the given figure, there are two rays :
● Ray → TA : This ray starts at point 'T' and is extended beyond point 'A'.
● Ray → TB : This ray starts at point 'T' and is extended beyond point 'B'.
Therefore, Yes point 'T' is the starting point of both rays.
Q4.
Draw a rough figure and write labels appropriately to illustrate each of the following:
a. Line (↔ OP) and Line (↔ OQ) meet at O.
Solution :

b. Ray (→ XY) and Line (↔ PQ) intersect at point M.
Solution :

c. Line l contains points E and F but not point D.
Solution :

d. Point P lies on AB.
Solution :

Q5.
In Fig. 2.6, name:

a. Five points
Answer : The five points in the figure are B, C, O, E and D.
b. A line
Answer : A line in the figure is ↔ DB.
c. Four rays
Answer : The four rays in the figure are → OD, → OB, → OC and → ED.
d. Five line segments
Answer : The Five line segments in the figure are DE, EO, OB, OC and OD.
Page 17 : Figure it out
Q6.
Here is a ray OA (Fig. 2.7). It starts at O and passes through the point A. It also passes through the point B.
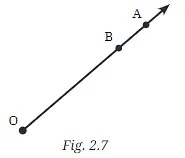
a. Can you also name it as OB ? Why?
Answer.
Yes, we can name it as 'OB' as the ray 'OA' passes through the point 'B'. A ray is drawn from a starting point 'O' is extended beyond the point 'B' as well as point 'A'. So it can be named both 'OA' and 'OB'.
b. Can we write OA as AO ? Why or why not?
Answer.
No, we can not write 'OA' as 'AO' because rays are directional. The ray starts at point 'O' and extended beyond point 'A', So 'OA' indicates the direction of the ray from point 'O' to point 'A'.
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 19.
Ganita Prakash Class 6 Maths Chapter 2 Solutions Lines and Angles.
Q1.
Can you find the angles in the given pictures? Draw the rays forming any one of the angles and name the vertex of the angle.


Solution :

● In ∠ADC, Rays are DA and DC. Vertex is D.

● In ∠POQ, Rays are OP and OQ. Vertex is O.

● In ∠EOF, Rays are OE and OF. Vertex is O.

● In ∠ABC, Rays are BA and BC. Vertex is B.
Page 20 : Figure it out.
Q2.
Draw and label an angle with arms ST and SR.
Solution :
With arms ST and SR the angle formed is ∠TSR.

Q3.
Explain why ∠APC cannot be labelled as ∠P.

Answer :
∠APC can not be labelled as ∠P because there are more than one angles at the vertex P i.e. ∠APB and ∠BPC.
Q4.
Name the angles marked in the given figure.

Answer :
The angles (∠) marked in the figure are -
● ∠PTR
● ∠QTR
Q5.
Mark any three points on your paper that are not on one line. Label them A, B, C. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C? Write them down, and mark each of them with a curve as in Fig. 2.9.
Solution :
We have 3 points A, B and C. By joining these 3 points we get 3 interconnected lines i.e. AB, BC and CA. Now, we get 3 angles (∠) between these 3 lines i.e. ∠ABC, ∠BCA and ∠CAB.

Page 21 : Figure it out.
Q6.
Now mark any four points on your paper so that no three of them are on one line. Label them A, B, C, D. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C, D? Write them all down, and mark each of them with a curve as in Fig. 2.9.
Solution :
We have 4 points A, B, C and D. By joining these 4 points we get 6 interconnected lines i.e. AB, BC, CD, DA, DB and AC. Now, we get 12 angles (∠) between these 4 lines i.e. ∠ABC, ∠BCD, ∠CDA, ∠DAB, ∠ABD, ∠BAC, ∠CBD, ∠BCD, ∠ACD, ∠BDC, ∠CAD and ∠ADB.

Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 23.
NCERT Solutions for Class 6 Maths Ganita Prakash Chapter 2 Lines and Angles
Q1.
Fold a rectangular sheet of paper, then draw a line along the fold created. Name and compare the angles formed between the fold and the sides of the paper. Make different angles by folding a rectangular sheet of paper and compare the angles. Which is the largest and smallest angle you made?

Answer :

The angles (∠'s) formed along the folded line are ∠AEF, ∠BEF, ∠DFE and ∠CFE. These angles (∠'s) are marked with number 1, 2, 3 and 4. Out of these angles ∠AEF and ∠CFE are the larger ones. On the other hand ∠BEF and ∠DFE are the smaller ones.
Q2.
In each case, determine which angle is greater and why.
a. ∠AOB or ∠XOY
b. ∠AOB or ∠XOB
c. ∠XOB or ∠XOC

Discuss with your friends on how you decided which one is greater.
Solution :
a. ∠AOB is greater than ∠XOY because ∠XOY is a part of ∠AOB.
b. ∠AOB is greater than ∠XOB because ∠XOB is a part of ∠AOB.
c. ∠XOB is equal to ∠XOC because the corners of both of these angles match and the arms overlap with each other.
Q3.
Which angle is greater: ∠XOY or ∠AOB? Give reasons.

Answer :
∠XOY is greater than ∠AOB because the distance (spread) between the two arms of ∠XOY is more than that of ∠AOB.
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 29.
Class 6 Maths Ganita Prakash Chapter 2 Lines and Angles Question Answers.
Q1.
How many right angles do the windows of your classroom contain? Do you see other right angles in your classroom?
Answer :

The window usually contain 4 right angles (∟) at each corner. The window of my classroom contains several right angles at the corners where frames meet at 90°. The other right angles in my classroom are present at the corners of the door, at tiles of the floor, on the desk and at blackboard. Right angles are present on these places as they are square and rectangular shaped.
Page 30 : Figure it out.
Q2.
Join A to other grid points in the figure by a straight line to get a straight angle. What are all the different ways of doing it?

Solution :
The other ways to form straight angles are :

Q3.
Now join A to other grid points in the figure by a straight line to get a right angle. What are all the different ways of doing it?

Solution :
The different ways to form right angle are :

Page 31 : Figure it out.
Q4.
Get a slanting crease on the paper. Now, try to get another crease that is perpendicular to the slanting crease.
a. How many right angles do you have now? Justify why the angles are exact right angles.
b. Describe how you folded the paper so that any other person who doesn’t know the process can simply follow your description to get the right angle.
Answer :

a. We will get 4 right angles (∟) because when we fold the paper perpendicular to the first crease, both the creases intersect each other at 90° which divides the plane into 4 right angles of 90° each.
b. Just Follow the process given below :
● Take a piece of paper and fold it diagonally from one corner to the corner of opposite side.
● Now, unfold the paper and fold it again diagonally with other two corners.
● Here, we get two creases intersecting each other at 90° angle.
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 15.
lines and angles class 6 ncert solutions.
Q1.
Identify acute, right, obtuse and straight angles in the previous figures.
Answer :

Q2.
Make a few acute angles and a few obtuse angles. Draw them in different orientations.
Answer :

Page 32 : Figure it out.
Q3.
Do you know what the words acute and obtuse mean? Acute means sharp and obtuse means blunt. Why do you think these words have been chosen?
Answer :
Yes, in mathematics acute and obtuse have a meaning :
● Acute : The word acute means 'sharp' in english. But in geometry it means an angle which has measurement of more than 0° and less than 90°. The acute angles are less than 90°. So, they appear sharp or narrow, that is why they are given the name 'ACUTE'.
● Obtuse : The word obtuse means 'blunt' in english. But in geometry it means an angle which has measurement of more than 90° and less than 180°. The obtuse angles are more than 90°. So, they appear blunt or broad, that is why they are given the name 'OBTUSE'.
Q4.
Find out the number of acute angles in each of the figures below.

What will be the next figure and how many acute angles will it have? Do you notice any pattern in the numbers?
Solution :

To find number of acute angles in the given figure we just need to count number of triangles in each figure and then just multiply it by 3.
● The number of acute angles in the figure 1 is 03.
● The number of acute angles in the figure 2 is 12.
● The number of acute angles in the figure 3 is 21.
● The number of acute angles in the figure 4 is 30.
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 35.
ncert class 6 maths chapter 2 lines and angles solutions.
Q1.
Write the measures of the following angles:

a. ∠ KAL
Notice that the vertex of this angle coincides with the centre of the protractor. So the number of units of 1 degree angle between KA and AL gives the measure of ∠KAL. By counting, we get ∠KAL = 30°.
Making use of the medium sized and large sized marks, is it possible to count the number of units in 5s or 10s?
b. ∠WAL = 50°
c. ∠TAK = 120°
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 40.
lines and angles class 6 ncert solutions chapter 2.
Q1.
Find the degree measures of the following angles using your protractor.

Answer :

● ∠IHJ = 47°
● ∠IHJ = 24°
● ∠IHJ = 110°
Q2.
Find the degree measures of different angles in your classroom using your protractor.
Answer :
The degree measures of different angles in my classroom are :
● Angles at the corner of classroom = 90°
● Angle between the floor and the wall = 90°
● Angle between the chair seat and backrest = 120°
● Dorr open halfway = 45°
Page 41 : Figure it out.
Q3.
Find the degree measures for the angles given below. Check if your paper protractor can be used here!

Answer :

● ∠JHI = 41°
● ∠JHI = 116°
No, paper protractor can not be used here.
Q4.
How can you find the degree measure of the angle given below using a protractor?

Answer :
We can find the degree measure of the given angle using a protractor by these steps :
● Measure the smaller angle with the help of protractor, then subtract it from 360°.
● On subtracting the smaller angle from 360° we get the the measure of larger angle. i.e.
- Measure of smaller angle = 100°
- Measure of complete angle = 360°
- Measure of required angle = 360° - 100° = 260°.
Q5.
Measure and write the degree measures for each of the following angles:

Answer :

(a) Measurement of given angle is 80°.
(b) Measurement of given angle is 120°.
(c) Measurement of given angle is 60°.
(d) Measurement of given angle is 130°.
(e) Measurement of given angle is 130°.
(f) Measurement of given angle is 60°.
Page 42 : Figure it out.
Q6.
Find the degree measures of ∠BXE, ∠CXE, ∠AXB and ∠BXC

Solution :
● Measurement of ∠BXE = 115°.
● Measurement of ∠CXE = 85°.
● Measurement of ∠AXB = 65°.
● Measurement of ∠BXC = 30°.
Q7.
Find the degree measures of ∠PQR, ∠PQS and ∠PQT.

Solution :
● Measurement of ∠PQR = 45°.
● Measurement of ∠PQS = 100°.
● Measurement of ∠PQT = 150°.
Page 43 : Figure it out.
Q8.
Make the paper craft as per the given instructions. Then, unfold and open the paper fully. Draw lines on the creases made and measure the angles formed.

Solution : Classroom Activity
Q9.
Measure all three angles of the triangle shown in Fig. 2.21 (a), and write the measures down near the respective angles. Now add up the three measures. What do you get? Do the same for the triangles in Fig. 2.21 (b) and (c). Try it for other triangles as well, and then make a conjecture for what happens in general! We will come back to why this happens in a later year.

Solution :

(a) In triangle △ABC :
● Measurement of ∠ABC = 65°.
● Measurement of ∠BAC = 45°.
● Measurement of ∠ACB = 70°.
Sum of all angles of triangle △ABC
= ∠ABC + ∠BAC + ∠ACB
= 65° + 45° + 70°
= 180°
(b) In triangle △ABC :
● Measurement of ∠ABC = 62°.
● Measurement of ∠BAC = 56°.
● Measurement of ∠ACB = 62°.
Sum of all angles of triangle △ABC
= ∠ABC + ∠BAC + ∠ACB
= 62° + 56° + 62°
= 180°
(c) In triangle △ABC :
● Measurement of ∠ABC = 55°.
● Measurement of ∠BAC = 30°.
● Measurement of ∠ACB = 95°.
Sum of all angles of triangle △ABC
= ∠ABC + ∠BAC + ∠ACB
= 55° + 30° + 95°
= 180°
∴ We have conjecture from the given activity that the sum of all the angles of any triangle (△) is always 180°.
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 45.
lines and angles class 6 question answer.
Where are the angles?
Q1.
Angles in a clock:
a. The hands of a clock make different angles at different times. At 1 o’clock, the angle between the hands is 30°. Why?
b. What will be the angle at 2 o’clock? And at 4 o’clock? 6 o’clock?
c. Explore other angles made by the hands of a clock.


Solution :
(a)
A clock is divided into 12 hours and the numbers 1 to 12 are written along the circumference of the clock at equal distances. Circumference of the circular clock is at 360°.
Therefore 360° ÷ 12 = 30°.
Hence, angle between two consecutive numbers is 30°.
Here, At 1 o'clock hands are at 12 and 1 (consecutive numbers)
Hence angle between them is 30°.
(b)
● Angle at 2 o'clock = 2 x 30° = 60°
● Angle at 4 o'clock = 4 x 30° = 120°
● Angle at 6 o'clock = 6 x 30° = 180°
(c)

● Angle at 3 o'clock = 3 x 30° = 90°
● Angle at 9 o'clock = 9 x 30° = 270°
● Angle at 5 o'clock = 5 x 30° = 150°
● Angle at 11 o'clock = 11 x 30° = 330°
Q2.
The angle of a door: Is it possible to express the amount by which a door is opened using an angle? What will be the vertex of the angle and what will be the arms of the angle?

Solution :
Yes, it is possible to express the amount by which a door is opened by using an angle. The hinge of the door will be the vertex of the angle. The wall and the door will be the arms of the angle.
Q3.
Vidya is enjoying her time on the swing. She notices that the greater the angle with which she starts the swinging, the greater is the speed she achieves on her swing. But where is the angle? Are you able to see any angle?

Solution :

Yes, we can see the angle and the angle is between the rope and the branch of the tree.
Page 46 : Figure it out.
Q4.
Here is a toy with slanting slabs attached to its sides; the greater the angles or slopes of the slabs, the faster the balls roll. Can angles be used to describe the slopes of the slabs? What are the arms of each angle? Which arm is visible and which is not?

Solution :

Yes, angles can be used to describe the slopes of the slabs. The slanting slab and the the invisible line that is perpendicular to the sides of the toy are two arms of each angle. The slanting slab is visible while the line perpendicular to the sides of the toy are not visible.
Q5.
Observe the images below where there is an insect and its rotated version. Can angles be used to describe the amount of rotation? How? What will be the arms of the angle and the vertex?
Hint: Observe the horizontal line touching the insects.

Answer :
Yes, angles can be used to describe the amount of rotation by observing the initial and the final position of the insect. The horizontal line and the insect itself will be the arm of the angle and the vertex will be the back end of the insect.
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 49.
lines and angles class 6 questions.
Q1.
In Fig. 2.23, list all the angles possible. Did you find them all? Now, guess the measures of all the angles. Then, measure the angles with a protractor. Record all your numbers in a table. See how close your guesses are to the actual measures.

Solution :
The angles in the given figure are :
| Angles | Guessed Measurement | Actual Measurement |
|---|---|---|
| ∠PAC | 110° | 107° |
| ∠ACD | 80° | 72° |
| ∠APL | 85° | 82° |
| ∠DLP | 110° | 98° |
| ∠RPL | 110° | 100° |
| ∠PLS | 90° | 83° |
| ∠LSR | 85° | 80° |
| ∠PRS | 110° | 103° |
| ∠BRS | 85° | 78° |
Page 50 : Figure it out.
Q2.
Use a protractor to draw angles having the following degree measures:
a. 110°
b. 40°
c. 75°
d. 112°
e. 134°
Solution :

Q3.
Draw an angle whose degree measure is the same as the angle given below:

Also, write down the steps you followed to draw the angle.
Solution :

The measure of the given angle is 120° and it can be drawn by the following steps :
- Draw a ray OA.
- Now, place the center point of the protractor on O and align the 0° line of protractor to ray OA.
- Now, starting from 0° count up to 120° and mark a point B and draw a line from O to B.
- Here, you get ∠AOB = 120°.
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 51.
lines and angles class 6 solutions.
Q1.
In each of the below grids, join A to other grid points in the figure by a straight line to get:
a. An acute angle

b. An obtuse angle

c. A reflex angle

Mark the intended angles with curves to specify the angles. One has been done for you.
Solution :
a. Acute angle :

b. Obtuse angle :

c. Reflex angle :

Page 52 : Figure it out.
Q2.
Use a protractor to find the measure of each angle. Then classify each angle as acute, obtuse, right, or reflex.
a. ∠PTR
b. ∠PTQ
c. ∠PTW
d. ∠WTP

Solution :
a. ∠PTR = 30°
b. ∠PTQ = 60°
c. ∠PTW = 105°
d. ∠WTP = 360° - 105° = 255°
Ganita Prakash class 6 maths chapter 2 lines and angles figure it out ncert page 53.
Ganita Prakash ncert solutions chapter 2.
Q1.
Draw angles with the following degree measures:
a. 140°
b. 82°
c. 195°
d. 70°
e. 35°
Solution :

Q2.
Estimate the size of each angle and then measure it with a protractor:

Classify these angles as acute, right, obtuse or reflex angles.
Solution :
| Estimated Angles | Actual Angles | |
|---|---|---|
| a. | 30° | 45° |
| b. | 150° | 165° |
| c. | 110° | 120° |
| d. | 25° | 32° |
| e. | 95° | 100° |
| f. | 350° | 350° |
- ● Acute angles : (a) & (d)
- ● Right angles : ---
- ● Obtuse angles : (b), (c), (e) & (f)
Q3.
Make any figure with three acute angles, one right angle and two obtuse angles.
Solution :

- ● 3 acute angles are ∠COD, ∠COB, ∠BOD
- ● 1 Right angle is ∠AOB
- ● 2 Obtuse angles are ∠AOD, ∠AOC
Q4.
Draw the letter ‘M’ such that the angles on the sides are 40° each and the angle in the middle is 60°.
Solution :

Q5.
Draw the letter ‘Y’ such that the three angles formed are 150°, 60° and 150°.
Solution :

Explanation :
The angles on both the sides of 'Y' are wide i.e. 150°, while the angle at the middle is narrow i.e. 60°.
Page 54 : Figure it out.
Q6.
The Ashoka Chakra has 24 spokes. What is the degree measure of the angle between two spokes next to each other? What is the largest acute angle formed between two spokes?

Answer :
The Ashoka chakra has 24 spokes and has a total of 360° circumference.
Therefore, To get the degree measure of angle between 2 spokes we need to divide 360° by 24 that is 15°. The largest acute angle formed between 2 spokes is 75°.
Q7.
Puzzle : I am an acute angle. If you double my measure, you get an acute angle. If you triple my measure, you will get an acute angle again. If you quadruple (four times) my measure, you will get an acute angle yet again! But if you multiply my measure by 5, you will get an obtuse angle measure. What are the possibilities for my measure?
Answer :
The possibilities of your measure are 19°, 20°, 21°, 22°.
Explanation :
To get the possible measures we need to divide largest acute angle by 4 that is 89° ÷ 4 = 22° approx. and now divide smallest obtuse angle by 5 that is 91° ÷ 5 = 19° approx.
# Worksheet - Extra Questions :
Lines and Angles Class 6 Extra Questions Maths Chapter 2.
lines and angles class 6 worksheet.
# Fill in the blanks :
1. A line segment has _______ endpoints.
2. An angle of exactly 90° is called a _______ angle.
3. A ray starts at one point and extends _______ in one directions.
4. A _______ is a tool used to measure an angle.
5. An angle that is greater than 90° but less than 180° is called _______ angle.
# True - False :
1. An obtuse angle is an angle that measures less than 90°.
2. A straight angle measures exactly 180°.
3. A reflex angle is greater than 90° but less that 360°.
4. A line has fixed length.
5. An angle measures 63° is an acute angle.
# Multiple Choice Questions :
Q1. Name an angle which measures 180°.
(a) straight angle
(b) Right angle
(c) reflex angle
(d) acute angle
Q2. Name an angle which measures 1°.
(a) acute angle
(b) reflex angle
(c) straight angle
(d) Right angle
Q3. Name an angle which measures 179°.
(a) obtuse angle
(b) Right angle
(c) straight angle
(d) reflex angle
Q4. Name an angle which measures 220°.
(a) reflex angle
(b) acute angle
(c) Right angle
(d) straight angle
Q5. Which type of angle is formed when a door is closed halfway?
(a) straight angle
(b) obtuse angle
(c) right angle
(d) acute angle
# Activity based Questions :
Q1. Draw an angle of 90° and label it as ∠ABC.
Q2. Draw an acute angle and label it as ∠XYZ.
Q3. Draw an obtuse angle and label it as ∠PQR.
Q4. Draw a straight angle and label it as ∠OBC.
Q5. Draw a complete angle and label it as ∠BOC.
# Numerical Question :
Q1.
Name the angles in the given figure.

(i) A line.
(ii) Four line segments with a common end-point.
(iii) Four rays having same starting points.
(iv) Five points.
Q2.
Name the angles in the given figure.

Q3.
Mrs. Sushma, a maths teacher is guiding her class, to identify angles in English alphabets, like three acute angles and two obtuse angles in A, two equal acute angle in letter N and so on.

Based on above information answer the following questions :
(a) Which letter represents only a right angle?
(b) Which letter represents only two straight angles?
(c) Which two letters represent only four right angles?
Q4.
Name the angles involved in the given figure.

Q5.
Name the kind of angles made with the hands of a clock when it show the time :
(a) 01:15
(b) 03:30
(c) 04:45
(d) 06:00
(e) 07:10
(f) 12:00
Class 6 Maths Chapter 2 Extra Questions Lines and Angles.
lines and angles class 6 worksheet with answers.
# Fill in the Blanks :
1. Two
2. Right
3. Endlessly
4. Protractor
5. Reflex
# True - False :
1. False
2. True
3. False
4. False
5. True
# MCQ's :
1. Straight angle (a)
2. Acute angle (a)
3. Obtuse angle (a)
4. Reflex angle (a)
5. Acute angle (d)
# Activity Base Questions :
Solution Q1 :

Solution Q2 :

Solution Q3 :

Solution Q4 :

Solution Q5 :

# Numerical Questions :
Solution Q1 :
- (i) A line = AD.
- (ii) Four line segments with common end-point are : OA, OB, OC and OD.
- (iii) Four rays are having same start point : OA, OB, OC and OD.
- (iv) O, A, B, C, and D are five points.
Solution Q2 :
The angles are:
- (i) ∠A or ∠DAB
- (ii) ∠B or ∠ABC
- (iii) ∠C or ∠DCB
- (iv) ∠D or ∠ADC
Solution Q3 :
(a) The letter ‘L’ represents a right angle.

(b) The letter I represents two straight angles.

(c) The letters ‘E’ and ‘H’ represents four right angles.

Solution Q4 :
The angles involved in the given figure are :

In △ABC : ∠ABC, ∠BCA, ∠CAB.
In △BFC : ∠BFC, ∠FCB, ∠FBC.
In △BFE : ∠BEF, ∠FBE, ∠BFE.
In △CFD : ∠CDF, ∠FCD, ∠CFD.
In quadrilateral ADFE : ∠DFE , ∠ADF, ∠AEF, ∠DAE.
Solution Q5 :
The kind of angles made with the hands of a clock when it show the time :
(a) 01:15

(b) 03:30

(c) 04:45

(d) 06:00

(e) 07:10

(f) 12:00

# MCQ Test :
Lines and Angles mcq :
# FAQ's :
A line segment is a part of a line that has two end points, while line has no end point it can extended indefinitely in both the directions.
The different types of angles are - Acute angle, Right angle, Obtuse angle, straight angle, reflex angle and complete angle.
Angles are measured in degrees using a geometrical tool called protractor.
Angles can be compared by measuring the distance between their two arms in degrees using a protractor.
We can differentiate between acute, obtuse and right angle by measuring their size in degree as measure of acute angle is less than 90°, whereas measure of right angle is exactly 90° and measure of obtuse angle is more than 90° but less than 180°.
# Still have some Doubts ?
-- Feel FREE to Ask your Doubts Here --
# Learn More :
CBSE Class 6th Mathematics teaches students about the basics, which have a wide range of application in their higher studies. All the chapters given below includes Solutions for all the question available in Class 6th Mathematics NCERT Textbook Ganita Prakash. It also includes some Important Extra Questions related to the Chapters and we have also provided Free Quiz Based Test which is consist of Objective Type Questions which help the students to test their Understanding about the given Chapters. This material is available for Free For the Students So that they can prepare & score good marks in their upcoming exams.
| Chapters | Class 6 Maths Syllabus |
|---|---|
| Chapter 01 : | Patterns in Mathematics |
| Chapter 02 : | Lines and Angles |
| Chapter 03 : | Number Play |
| Chapter 04 : | Data Handling and Presentation |
| Chapter 05 : | Prime Time |
| Chapter 06 : | Perimeter and Area |
| Chapter 07 : | Fractions |
| Chapter 08 : | Playing with Constructions |
| Chapter 09 : | Symmetry |
| Chapter 10 : | The Other Side of Zero |
Curiosity, Textbook of Science for Grade 6, comprises twelve chapters. As the name of the textbook suggests, there are numerous opportunities for the learners to explore the world of science and its nature. Through the chapters, learners will embark on a journey that will connect them to the world around and spark curiosity for further exploration. The hands-on activities embedded within each chapter engages the learners and provide them an opportunity to reflect on learning. The primary aim of Curiosity is to prepare the children for becoming the responsible members of the society, and therefore efforts have been made to raise awareness about various issues, such as gender, region, environment, health and hygiene, water scarcity and energy conservation.
| Chapters | Class 6 Science Syllabus |
|---|---|
| Chapter 01 : | The Wonderful World of Science |
| Chapter 02 : | Diversity in the Living World |
| Chapter 03 : | Mindful Eating: A Path to a Healthy Body |
| Chapter 04 : | Exploring Magnets |
| Chapter 05 : | Measurement of Length and Motion |
| Chapter 06 : | Materials Around Us |
| Chapter 07 : | Temperature and its Measurement |
| Chapter 08 : | A Journey through States of Water |
| Chapter 09 : | Methods of Separation in Everyday Life |
| Chapter 10 : | Living Creatures: Exploring their Characteristics |
| Chapter 11 : | Nature’s Treasures |
| Chapter 12 : | Beyond Earth |
Class 6th English NCERT Poorvi has five thematic units that comprise stories, poems, conversation, narrative and descriptive pieces. Themes such as friendship, wellness, sports, nature, art and culture, etc. have been included. Cross-cutting themes, such as Indian Knowledge Systems, values, heritage, gender sensitivity and inclusion have been integrated in all the units. Each unit has three literary pieces― story or conversation, poem and non-fiction. There are intext questions, ‘Let us discuss’ to assess comprehension of the text. The end-of-the-text questions given in ‘Let us think and reflect’ are designed to encourage critical thinking, reasoning, responding, analyzing, etc. These literary pieces are not only entertaining but also instill valuable life lessons, fostering personal growth and helping children navigate social situations with confidence. The selected pieces will resonate with children’s daily experiences and encourage positive values like resilience, empathy and emotional intelligence that can have a profound impact on their development.
| No. | Class 6 English Syllabus |
|---|---|
| Unit 1 : | Fables and Folk Tales |
| A Bottle of Dew | |
| The Raven and The Fox | |
| Rama to the Rescue | |
| Unit 2 : | Friendship |
| The Unlikely Best Friends | |
| A Friend's Prayer | |
| The Chair | |
| Unit 3 : | Nurturing Nature |
| Neem Baba | |
| What a Bird Thought | |
| Spices that Heal Us | |
| Unit 4 : | Sports and Wellness |
| Change of Heart | |
| The Winner | |
| Yoga - A Way of Life | |
| Unit 5 : | Culture and Tradition |
| Hamara Bharat - Incredible India! | |
| The Kites | |
| Ila Sachani : Embroidering Dreams with her Feet | |
| National War Memorial |


